cppmat::cartesian¶
Provides classes for 4th- and 2nd order tensors and vectors. For example, a fourth order identity tensor in 3-D is obtained as follows:
#include <cppmat/cppmat.h>
int main()
{
cppmat::cartesian::tensor4<double> A = cppmat::cartesian::tensor4<double>::I(3);
...
std::cout << A << std::endl;
return 0;
}
Tip
If you know that you will work in a fixed (and small) number of dimensions (e.g. 2 or 3), please consider using cppmat::tiny::cartesian instead of cppmat::cartesian. This is generally more efficient as it can take advantage of the knowledge that the arrays are fixed size and relatively small. Also several loops are unrolled.
Tip
The notation can be shortened to:
#include <cppmat/cppmat.h>
using T4 = cppmat::cartesian::tensor4<double>;
int main()
{
T4 A = T4::I(3);
...
return 0;
}
Classes¶
cppmat::cartesian::tensor4¶
[var_cartesian_tensor4.h, var_cartesian_tensor4.hpp]
4th-order tensor (rank 4 tensor) of arbitrary dimension.
cppmat::cartesian::tensor4<double> A(3);
A(0,0,0,0) = ...
cppmat::cartesian::tensor2¶
[var_cartesian_tensor2.h, var_cartesian_tensor2.hpp]
2nd-order tensor (rank 2 tensor) of arbitrary dimension.
cppmat::cartesian::tensor2<double> A(3);
A(0,0) = ...
cppmat::cartesian::tensor2s¶
[var_cartesian_tensor2s.h, var_cartesian_tensor2s.hpp]
Symmetric 2nd-order tensor.
cppmat::cartesian::tensor2s<double> A(3);
A(0,0) = ...
For example, for the case of 3 dimensions, the following components are stored:
[ X , X , X ;
X , X ;
X ]
The remaining components are inferred from symmetry. See cppmat::symmetric::matrix.
cppmat::cartesian::tensor2d¶
[var_cartesian_tensor2d.h, var_cartesian_tensor2d.hpp]
diagonal 2nd-order tensor.
cppmat::cartesian::tensor2d<double> A(3);
A(0,0) = ...
For example, for the case of 3 dimensions, the following components are stored:
[ X ;
X ;
X ]
The remaining components are imposed to be zero. See cppmat::diagonal::matrix.
cppmat::cartesian::vector¶
[var_cartesian_vector.h, var_cartesian_vector.hpp]
Vector (rank 1 tensor) of arbitrary dimension. For example:
cppmat::cartesian::vector<double> A(3);
A(0) = ...
Note
Because of the flexibility of C++ it is easy to switch between these specialized classes and the more general cppmat::cartesian::tensor2 classes. For example, the following will work:
using T2 = cppmat::cartesian::tensor2 <double>;
using T2d = cppmat::cartesian::tensor2d<double>;
T2d I = T2d::I(3);
T2 A = I;
or even
T2 I = T2d::I(3);
Also arithmetic works:
T2d A = 3.0 * I;
Note that it is even possible to perform arithmetic between the three different 2nd-order tensor classes, whereby the output type depends on the type of operator.
Finally, all the Methods accept all three classes - cppmat::cartesian::tensor2, cppmat::cartesian::tensor2s, cppmat::cartesian::tensor2d - allowing their usage without any prior type casting. In fact the methods will often perform better for the specialized classes since fewer operations are needed.
Note
The easy automatic conversion described above is not possible from a class to another where more assumptions on the structure are made (e.g. from cppmat::cartesian::tensor2 to cppmat::cartesian::tensor2d) because information is (potentially) lost.
Methods¶
All the methods of cppmat::array (or cppmat::matrix, cppmat::symmetric::matrix, cppmat::symmetric::matrix, or cppmat::vector) are overloaded. In addition, the following tensor algebra is available.
Note
Below the rank can be inferred from the indices, but should be easy to understand even without them. Pseudo-code is used to introduce the methods. For the first method it is short for:
cppmat::cartesian::tensor4<double> A = cppmat::cartesian::tensor4<double>::I(3);
cppmat::cartesian::tensor2<double> B = cppmat::cartesian::tensor2<double>::I(3);
cppmat::cartesian::tensor2<double> C = A.ddot(B);
Finally, each occurrence of cppmat::cartesian::tensor2 can be replaced by cppmat::cartesian::tensor2s or cppmat::cartesian::tensor2d. The latter two often perform better.
cppmat::cartesian::tensor4<X>:cppmat::cartesian::tensor4<X> C = A.ddot(const cppmat::cartesian::tensor4<X> &B)Double tensor contraction :
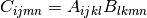
cppmat::cartesian::tensor2<X> C = A.ddot(const cppmat::cartesian::tensor2<X> &B)Double tensor contraction
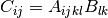
cppmat::cartesian::tensor4<X> C = A.T()Transposition
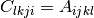
cppmat::cartesian::tensor4<X> C = A.LT()Left transposition
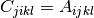
cppmat::cartesian::tensor4<X> C = A.RT()Right transposition
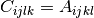
cppmat::cartesian::tensor2<X>:cppmat::cartesian::tensor2<X> C = A.ddot(const cppmat::cartesian::tensor4<X> &B)Double tensor contraction
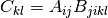
X C = A.ddot(const cppmat::cartesian::tensor2<X> &B)Double tensor contraction
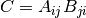
cppmat::cartesian::tensor2<X> C = A.dot(const cppmat::cartesian::tensor2<X> &B)Tensor contraction
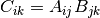
cppmat::cartesian::vector<X> C = A.dot(const cppmat::cartesian::vector<X> &B)Tensor contraction
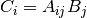
cppmat::cartesian::tensor4<X> C = A.dyadic(const cppmat::cartesian::tensor2<X> &B)Dyadic product
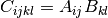
cppmat::cartesian::tensor2<X> C = A.T()Transposition
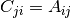
X C = A.trace()The trace of the tensor (i.e. the sum of the diagonal components)
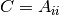
X C = A.det()The determinant
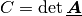
cppmat::cartesian::tensor2<X> C = A.inv()The inverse
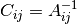
cppmat::cartesian::vector<X>:X C = A.dot(const cppmat::cartesian::vector<X> &B)Tensor contraction

cppmat::cartesian::vector<X> C = A.dot(const cppmat::cartesian::tensor2<X> &B)Tensor contraction
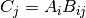
cppmat::cartesian::tensor2<X> C = A.dyadic(const cppmat::cartesian::vector<X> &B)Dyadic product
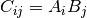
cppmat::cartesian::vector<X> C = A.cross(const cppmat::cartesian::vector<X> &B)Cross product
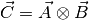
Note
One can also call the methods as functions using cppmmat::ddot(A,B), cppmmat::dot(A,B), cppmmat::dyadic(A,B), cppmmat::cross(A,B), cppmmat::T(A), cppmmat::RT(A), cppmmat::LT(A), cppmmat::inv(A), cppmmat::det(A), and cppmmat::trace(A). This is fully equivalent (in fact the class methods call these external functions).